Difference between revisions of "Keyboard"
| Line 16: | Line 16: | ||
If you want to borrow the Das Keyboard 4Q, please contact the Technical Support Group. Please note that the Das Keyboard Q software must be installed on a computer for the keyboard backlights to work. | If you want to borrow the Das Keyboard 4Q, please contact the Technical Support Group. Please note that the Das Keyboard Q software must be installed on a computer for the keyboard backlights to work. | ||
| − | [https://www.daskeyboard.io/get-started/ Detailed information] about programming the Das Keyboard 4Q can be found on the manufacturer website. A few exmples are given | + | [https://www.daskeyboard.io/get-started/ Detailed information] about programming the Das Keyboard 4Q can be found on the manufacturer website. A few exmples are given below. |
=== Setting key backlights from Python === | === Setting key backlights from Python === | ||
Revision as of 11:19, 3 July 2020
Corsair Vengeance K70
Most labs have one or more Corsair Vengeance K70 keyboards.
The backlights can be turned on and off with the keys on the top row:
- Use the round key in the center of the top row marked with a sun to set the keyboard backlight level in 4 steps.
- Use the round key in the left of the top row marked with a keyboard to switch between backlight on and programmed backlight.
- Press and hold the round key in the left of the top row marked with a keyboard to change which keys are on and which keys are off in programmed mode. Watch this video for a demonstration.
You can for instance program the keys to
Das Keyboard 4Q
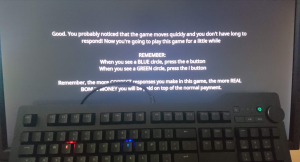
The Das keyboard allows far more advanced programming of keys. The photo on the right shows how the Das Keyboard can be programmed to react to the key mapping of the experiment. Some participants are instructed to press the E key for a green stimulus and the I key for a blue stimulus. For other participants it is the other way around. These instructions are shown at the start of the experiment. The keyboard backlights are used as a constant reminder of the instructions.
If you want to borrow the Das Keyboard 4Q, please contact the Technical Support Group. Please note that the Das Keyboard Q software must be installed on a computer for the keyboard backlights to work.
Detailed information about programming the Das Keyboard 4Q can be found on the manufacturer website. A few exmples are given below.
Setting key backlights from Python
#!/usr/bin/env python3
url = 'http://localhost:27301'
headers = { "Content-type": "application/json"}
import json
import requests
# prepare signal
signal = {
'zoneId': 'KEY_Q',
'color': '#F0F',
'effect': 'SET_COLOR',
'pid': 'DK4QPID',
'name': 'Set Q to purple'
}
# send signal
result = requests.post(url + '/api/1.0/signals', data=json.dumps(signal), headers=headers)
# checking the response
if result.ok:
print("OK")
print(result.text)
else:
print("Error: " + result.text)